Разбор с ФИПИ: типичные ошибки в ЕГЭ по базовой математике
ФИПИ проанализировала все работы, написанные в 2019 году, и составила список ошибок, которые чаще всего допускают выпускники. «УралСтудент» собрал самое главное из доклада ФИПИ по каждому предмету, а также разобрал задания, которые тяжело даются сдающим.
В 2015 году ЕГЭ по математике разделили на уровни: профильный и базовый. Базовый сдавали те, кому этот предмет нужен только для получения школьного аттестата. Профильную математику выбирали ребята, которым этот предмет необходим для поступления в вуз. Можно было писать сразу два варианта. Так выпускники могли обезопасить себя на случай, если на профильном уровне они не смогут пройти минимальный порог.
С 2019 года экзаменуемые выбирают только один вариант ЕГЭ по математике. Это нововведение значительно повлияло на результаты обоих экзаменов. В ЕГЭ по базовой математике наблюдается небольшое снижение результатов, поскольку не было выпускников, которые прежде планировали использовать его как «пробный» перед профильным.
Как выглядит ЕГЭ по базовой математике
КИМы по базовой математике состоят из 20 заданий с кратким числовым ответом или ответом в виде последовательности цифр. Экзамен проверяет знания базовых умений, включая бытовые расчёты, наглядную геометрию, владение приёмами вычислений и нахождения значений элементарных функций. Вариант содержит две задачи, требующие логического анализа и построения предложенной числовой конструкции.
Где большего всего допускали ошибки
Выпускники этого года плохо справились с заданием 13, где была стереометрическая задача. Также низкий процент выполнения наблюдается у задания 10 на вычисление вероятности, у заданий с задачамии 14–16, 19 и 20. Задача 14 на наглядное представление о производной. Геометрические задачи 15 и 16 на соотношения в прямоугольном треугольнике и расчёт элемента фигуры в пространстве. Задачи 19 и 20 требуют организованного перебора вариантов или логического анализа.
Задание 10
На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 9 прыгунов из России и 12 прыгунов из Китая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что третьим будет выступать прыгун из Китая.
Неверный ответ 0,25 мог быть получен делением числа 3 (порядковый номер спортсмена) на 12 (число прыгунов из Китая). Такой ответ говорит о том, что выпускник не понимает смысла данных чисел и своих действий.
При решении задач на поиск вероятности в опытах с равновозможными исходами следует придерживаться простого методического алгоритма.
1) Элементарным событием является выбор спортсмена для выступления третьим. Всего спортсменов N = 50.
2) Событию «для выступления третьим выбран спортсмен из Китая» благоприятствует M =12 выборов спортсмена.
3) Вероятность равна M/N = 12/50 = 0,24.
Задание 13

Эффект «промежуточного ответа». Найдя суммарный объём воды и детали, участник записал в ответ его вместо разности. Ошибка массовая и может проявиться в любой момент в любой задаче.
В базовом экзамене, где у участников нет дефицита времени, важно проверять и перепроверять решение и ответы. Необходимо учить школьников выполнять проверку ответов с точки зрения здравого смысла, полноты проведённых действий. Нужно проверять, верно ли переписано число с черновика и т.п. Наиболее эффективна отложенная проверка, выполненная не сразу же после решения задачи, а спустя некоторое время.
Задание 14
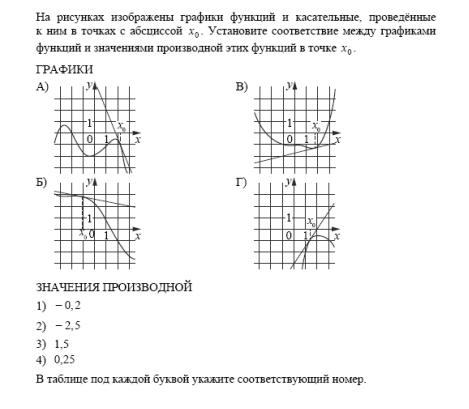
Типичные ошибки связаны с неверным сравнением модуля производной с единицей. Чтобы решить эту задачу, нужно разбить её на три этапа. Первый: определение знака производной; второй: сравнение наклона касательной с углом 45° позволит сравнить модуль производной с единицей. Необходимые пометки можно делать прямо на чертеже в КИМ. Третий этап: поиск производной по клеткам или установление соответствия.
Задание 16

Неверный ответ 12 получен, скорее всего, не за счёт ошибочного коэффициента в формуле объема конуса, а как результат деления 24 на 2.
Ответ 2 – результат некритического использования пояснительного рисунка в качестве точного чертежа. В обоих случаях участник пытался дать хоть какой-нибудь ответ, не зная, как решить задачу.
В данном случае важно донести до ученика, что рисунок в геометрии облегчает понимание взаимного расположения элементов, но не является чертежом с указанными размерами.
Задание 17

Трудность этого задания оказалась в понимании того, как ведут себя квадратный корень и квадрат числа меньшего или большего единицы. На это нужно обратить внимание. Квадрат числа не всегда больше самого числа, а корень – не всегда меньше.
Задание 19
Найдите трёхзначное натуральное число, большее 800, которое делится на каждую свою цифру и все цифры которого различны и не равны нулю. В ответе укажите какое-нибудь одно такое число.
Задание творческое, конструктивное, требующее не столько фантазии, сколько тщательного системного подбора, основанного на владении свойствами целых чисел. Если не использовать алгебраические соображения, то одно какое-нибудь число, удовлетворяющее всем условиям, можно найти минут за 5–10 простым перебором.
Эксперты отмечают, что многие школьники, понимая, что требуется в задаче, не способны проверить выполнение всех условий. В этой задаче непроверенным условием оказалось условие «делится на каждую свою цифру». Поэтому нужно тщательно и систематически последовательно проверить все условия, которые даны.
Задание 20
В доме всего десять квартир с номерами от 1 до 10. В каждой квартире живёт не менее одного и не более трёх человек. В квартирах с 1-й по 8-ю включительно живёт суммарно 10 человек, а в квартирах с 7-й по 10-ю включительно живёт суммарно 10 человек. Сколько всего человек живёт в этом доме?
Неверный ответ 20 получен сложением 10 и 10. Намного более интересен ответ 18, где школьники решили, что нужно удалить из квартир 7 и 8 «лишнего жильца», посчитанного дважды. В этом есть смысл, но только нужно учесть, что «лишних жильцов» в квартире может быть более одного.
Разбор с ФИПИ: типичные ошибки в ЕГЭ по профильной математике
Разбор с ФИПИ: типичные ошибки в ЕГЭ по русскому языку
Разбор с ФИПИ: типичные ошибки в ЕГЭ по литературе
Разбор с ФИПИ: типичные ошибки в ЕГЭ по информатике
Разбор с ФИПИ: типичные ошибки в ЕГЭ по биологии
Разбор с ФИПИ: типичные ошибки в ЕГЭ по обществознанию
Разбор с ФИПИ: типичные ошибки в ЕГЭ по истории
Разбор с ФИПИ: типичные ошибки в ЕГЭ по химии
Разбор с ФИПИ: типичные ошибки в ЕГЭ по физике
